Koen Derks en Lotte Mensink

Het doel van machine learning is om voorspellingen te maken aan de hand van data. Binnen dit veld worden doorgaans drie hoofdtoepassingen onderscheiden: classificatie, regressie en clusteren. In de vorige twee columns is er gekeken naar classificatie en regressie. Deze column gaat over clusteren.

De drie hoofdtoepassingen van machine learning kunnen worden opgedeeld in twee categorieën: begeleid leren (supervised learning) en onbegeleid leren (unsupervised learning). Welke hoofdtoepassing bij welke categorie hoort, is in onderstaande tabel aangegeven met een vinkje.

Begeleid leren houdt in dat je een algoritme voorziet van bepaalde kenmerken en de bijbehorende uitkomst, met als doel dat het algoritme de relatie tussen deze kenmerken en de uitkomst leert. Classificatie en regressie zijn typische voorbeelden hiervan. De eerste column behandelt een classificatiealgoritme, dat op basis van klantkenmerken voorspelt of een klant in het komende jaar een contract zal opzeggen. Op dezelfde wijze behandelt de tweede column een regressiealgoritme, dat op basis van bouwtechnische kenmerken de verkoopprijs van een woning voorspelt. Deze algoritmes worden dus gebruikt om de relatie tussen de kenmerken en de uitkomst te leren en daarmee vervolgens voorspellingen te maken. De informatie die voortkomt uit deze voorspellingen, kun je gebruiken om de audit verder in te richten.

Naast begeleid leren bestaat er ook onbegeleid leren. Dit is een vorm van machine learning waarbij je een algoritme patronen laat ontdekken in gegevens, zonder dat er een specifieke uitkomstvariabele meespeelt. Clusteren is een vorm van onbegeleid leren. Het doel van clusteren is om groepsstructuur te ontdekken in de gegevens, op basis van een aantal numerieke en/of categorische kenmerken. Deze techniek kun je nuttig toepassen in een audit. Je kunt clusteren bijvoorbeeld gebruiken om klanten van een online platform te groeperen op basis van verschillende kenmerken zoals koopgedrag, demografische gegevens en interacties met bedrijfsdiensten. Dit kan helpen bij het identificeren van risico's voor specifieke klantsegmenten. Daarnaast kun je clusteren bijvoorbeeld gebruiken bij een financiële instelling om rekeninghouders te identificeren die een afwijkende combinatie van kenmerken vertonen. Denk hierbij aan een afwijkende combinatie van leeftijd, het aantal contante opnames of stortingen en het aantal buitenlandse transacties. Bij deze rekeninghouders kan dan worden onderzocht of er sprake is van een ongebruikelijke transactie en mogelijk fraude.

'Het doel van clusteren is om groepsstructuur te ontdekken in de gegevens, op basis van een aantal numerieke en/of categorische kenmerken.'

In deze column demonstreren we hoe je met het gratis open-source statistiekprogramma JASP (JASP Team, 2024) zonder enige programmeerkennis een machine learning algoritme voor clusteren kunt toepassen in de context van een audit. We illustreren dit aan de hand van een voorbeeld, waarbij je als auditor bedrijfslocaties van een opslagruimteverhuurder wilt clusteren op basis van een aantal kenmerken.

Stel je voor dat je een audit uitvoert voor een bedrijf dat zich bezighoudt met de verhuur van opslagruimtes, verspreid over diverse locaties in het hele land. Als onderdeel van deze audit wil je de gerapporteerde omzet van de bedrijfslocaties controleren op juistheid. Om met een bepaalde mate van zekerheid een uitspraak hierover te kunnen doen, wil je een steekproef toepassen. Dit houdt in dat je een selectie van willekeurige bedrijfslocaties bezoekt ter controle van de administratie. Door de bedrijfslocaties te clusteren, kun je je auditwerkzaamheden beter inrichten door te focussen op de bedrijfslocaties met de hoogste risico’s. Zo kun je bijvoorbeeld een relatief kleine steekproef nemen in de bedrijfslocaties die een laag risico op administratieve fouten hebben en een relatief grotere in de locaties met een hoog risico. Op deze manier kun je je tijd en personeel efficiënter inzetten.

Om het voorbeeld concreet te maken gebruiken we een voor deze column licht bewerkte versie van de algemeen toegankelijke Pistil Storage-dataset*. De gegevens bevatten kenmerken van 1.531 bedrijfslocaties van de opslagruimteverhuurder, waaronder de gerapporteerde omzet, het aantal beschikbare opslageenheden en het aantal FTE's dat werkt aan de administratie**. Je wilt in de audit van de opslagruimteverhuurder stratificatie toepassen door een algoritme te gebruiken om de bedrijfslocaties op basis van deze kenmerken te clusteren.

Stratificatie

Stratificatie houdt in dat een populatie wordt onderverdeeld in subpopulaties, ook wel strata genoemd (Touw & Hoogduin, 2012, pagina 219).

'Bij een gestratificeerde steekproef is het dus noodzakelijk om de populatie op te delen in verschillende strata die intern vergelijkbaar zijn, maar onderling verschillend.'

Dit is nuttig bij het nemen van een steekproef uit een heterogene populatie. Door een populatie met een relatief grote spreiding in fouten op te splitsen in strata met een kleinere spreiding, kun je namelijk een meer nauwkeurige schatting van de fout maken bij een gegeven steekproefgrootte. Omgekeerd betekent dit dat je de gewenste zekerheid kan bereiken met een kleinere steekproef dan wanneer je niet zou stratificeren. In dergelijke situaties kun je daardoor eerder tot een beslissing komen, bijvoorbeeld goedkeuring, wat de efficiëntie van het steekproefproces verhoogt.

Bij een gestratificeerde steekproef is het dus noodzakelijk om de populatie op te delen in verschillende strata die intern vergelijkbaar zijn, maar onderling verschillend. In de context van het voorbeeld zou je dus bedrijfslocaties die veel op elkaar lijken in dezelfde strata willen indelen, terwijl je bedrijfslocaties die veel van elkaar verschillen in verschillende strata wil indelen. Dit kan op een regelgebaseerde manier worden gedaan op basis van kenmerken van de bedrijfslocaties, zoals de omzet. Om dit op een datagedreven manier te doen, kun je een clusteralgoritme gebruiken.

Clusteren

Een clusteralgoritme gaat uit van het idee dat er een bepaalde groepsstructuur te ontdekken is in de kenmerken van de bedrijfslocaties. Deze algoritmen functioneren door de gegevensruimte te verkennen en groepen, of 'clusters', van bedrijfslocaties te identificeren die vergelijkbare combinaties van kenmerken hebben. Wat precies als 'vergelijkbaar' wordt beschouwd, hangt af van het specifieke clusteralgoritme dat je gebruikt. Clustering kan bijvoorbeeld gebaseerd zijn op de afstand tussen kenmerken in een multidimensionale ruimte, of op de dichtheid van kenmerken in deze ruimte.

Hoewel de methodiek kan verschillen, is de uitkomst van een clusteralgoritme altijd vergelijkbaar: een set clusters waarbinnen de bedrijfslocaties combinaties van kenmerken hebben die meer op elkaar lijken dan op de combinaties van kenmerken van bedrijfslocaties in andere clusters. Het is hierbij belangrijk om te benadrukken dat clusteren een ander doel heeft dan classificatie. Je bent in deze context namelijk niet op zoek naar een ‘correct’ aantal clusters. In de praktijk wil je verschillende opties proberen en zoek je naar de meest nuttige of best interpreteerbare groepsindeling.

Hoewel een clusteralgoritme dus een aantal clusters identificeert, is het aan de auditor om te bepalen of deze clusters interpreteerbaar zijn en of er betekenis aan kan worden toegekend. In het volgende hoofdstuk bespreken we eerst hoe de auditor de clusters statistisch kan identificeren en interpreteren. Daarna behandelen we de bedrijfsmatige interpretatie van de clusters.

Toepassen clusteralgoritme

Het toepassen van een clusteralgoritme kun je doen in JASP door eerst JASP te downloaden van www.jasp-stats.org en te installeren. Na het inladen van de gegevens in JASP kun je de Machine Learning module inschakelen, door op het '+'-symbool in de rechterbovenhoek te klikken en 'Machine Learning' te kiezen. Hierdoor verschijnt de module in het menu boven in het scherm. Door vervolgens op de module te klikken, kun je alle functionaliteiten zien die de module aanbiedt. Via het menu in de linkerbovenhoek (Preferences - Interface - Preferred language) kun je daarnaast instellen dat de interface en de resultaten in het Nederlands worden weergegeven.

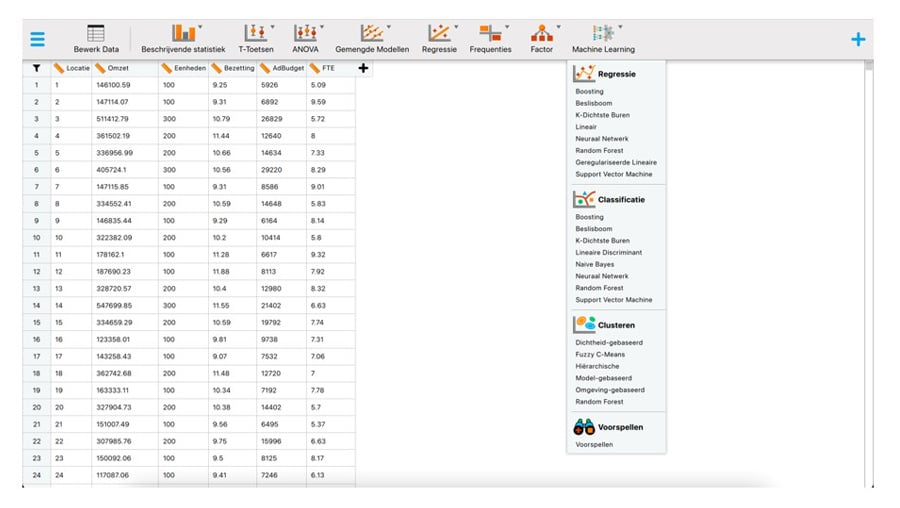
Zoals te zien is in de bovenstaande afbeelding zijn er voor het identificeren van groepsstructuur in de kenmerken van de bedrijfslocaties verschillende clusteralgoritmes beschikbaar. In deze column maken we gebruik van een zogenaamd random forest algoritme (James et al., 2023, pagina's 346-347). Dit algoritme creëert meerdere beslissingsbomen, elk gebaseerd op een wisselend deel van de gegevens, waarbij de uiteindelijke toewijzing van bedrijfslocaties aan clusters wordt vastgesteld door de meerderheidsstemming van deze beslisbomen. Om dit algoritme in JASP te gebruiken, selecteer je in het Machine Learning menu de optie 'Random Forest' onder 'Clusteren'.

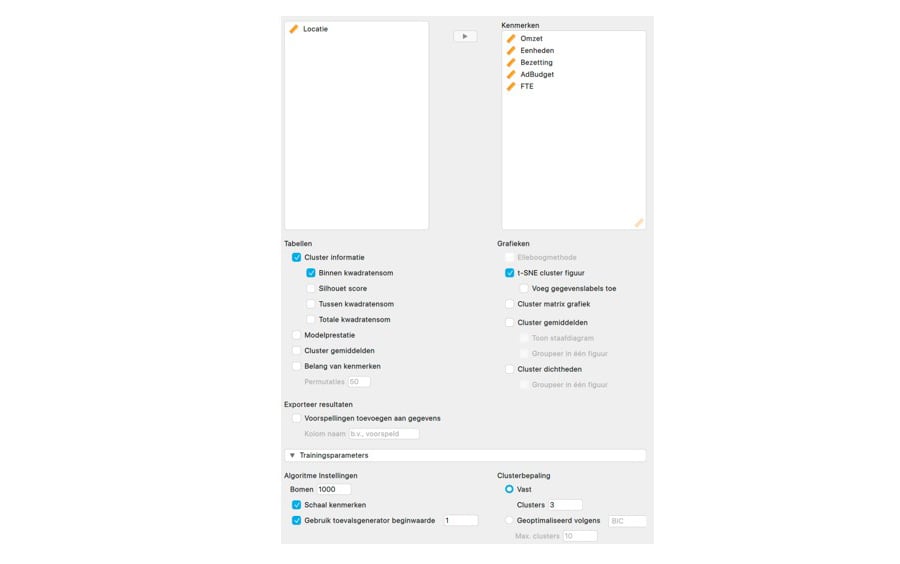
In de hieronder weergegeven interface vink je allereerst de optie 't-SNE cluster figuur' aan onder het kopje 'Grafieken'. Hiermee geef je aan dat je de verschillende clusters grafisch wilt laten weergeven. Daarna vouw je de sectie 'Trainingsparameters' open en selecteer je de optie 'Vast' onder het kopje 'Clusterbepaling', zodat het algoritme het standaard ingevulde aantal van drie clusters gaat bepalen. Je kunt hier ook zelf het aantal clusters instellen of het optimale aantal clusters door het algoritme laten bepalen. Vink in deze sectie ook meteen de optie 'Gebruik toevalsgenerator beginwaarde' aan. Daarmee stel je de willekeurige getallengenerator voor het clusteralgoritme in op de waarde 1, zodat de resultaten reproduceerbaar zijn op je eigen computer. Vervolgens sleep je alle kenmerken, behalve Locatie, naar het vak voor 'Kenmerken'.

Zodra alle data zijn ingevoerd, start JASP met het toepassen van het clusteralgoritme. De resultaten worden hieronder getoond. De bovenste tabel biedt inzicht in de input voor het algoritme, zoals het aantal clusters dat we het algoritme hebben laten bepalen (3) en het totale aantal datapunten (1.531). Daarnaast laat het statistieken zien die iets zeggen over de kwaliteit van de output van het algoritme, zoals bijvoorbeeld de determinatiecoëfficiënt R². In de vorige column over regressie is uitgelegd dat deze waarde een maatstaaf is voor de verklaarde variantie van een statistisch model. In een clusteringcontext betekent een R²-waarde van 0,541 dat het clusteringmodel 54,1 procent van de totale variantie in de gegevens kan verklaren. Met andere woorden: de door het model gevormde clusters verklaren ongeveer 54,1 procent van de spreiding in de datapunten rond de clustergemiddelden. De overige statistieken (AIC, BIC en silhouet score) kun je gebruiken om modellen met een verschillend aantal clusters te vergelijken. Voor het gemak gaan we daar in deze column niet op in, maar werken we met een vast aantal clusters.

De tweede tabel in de output toont informatie over de clusters. Deze clusterinformatietabel laat zien dat 499 van de 1.531 locaties in de dataset zijn toegewezen aan de eerste cluster, terwijl 543 en 489 locaties respectievelijk zijn toegewezen aan de tweede en derde cluster. In de tweede en derde regel van de tabel kun je de binnen-cluster kwadratensom zowel in percentages als in absolute getallen aflezen. De binnen-cluster kwadratensom is een maatstaf die de spreiding van de gegevens binnen elke cluster aangeeft. Als je deze waarde uitdrukt als een percentage van de totale variantie in de gegevens, krijg je de verklaarde proportie binnen-cluster heterogeniteit. Deze maatstaf ligt tussen 0 en 1 en kan nuttig zijn om het relatieve belang of ‘gewicht’ van elk cluster te begrijpen. Een hoge waarde van de verklaarde proportie binnen-cluster heterogeniteit duidt op een cluster met veel variantie, mogelijk door een groot aantal datapunten of een grote spreiding van datapunten, terwijl een lage waarde duidt op een meer compacte cluster. In dit geval verklaart de tweede cluster ongeveer veertig procent van de totale verklaarde variantie, terwijl de eerste en de derde cluster elk ongeveer dertig procent van de totale variantie verklaren.

Het laatste element in de output is een tweedimensionale weergave van de kenmerken van de bedrijfslocaties, bekend als de t-SNE clustergrafiek. Het t-SNE algoritme is ontworpen om bedrijfslocaties, die vergelijkbaar zijn op basis van hun kenmerken, te projecteren naar punten die dicht bij elkaar liggen in de tweedimensionale ruimte. Tegelijkertijd worden bedrijfslocaties, die sterk verschillen in hun kenmerken, geprojecteerd naar punten die verder uit elkaar liggen in deze tweedimensionale ruimte. Deze visualisatie kan nuttig zijn om te bepalen hoeveel clusters je zou kunnen maken bij het opdelen van de gegevens. De t-SNE grafiek hieronder laat bijvoorbeeld drie te onderscheiden groepen van bedrijfslocaties zien die sterk op elkaar lijken. Dit geeft aan dat de drie clusters die we het algoritme hebben laten bepalen een goede representatie zijn van de groepsstructuur in de gegevens.

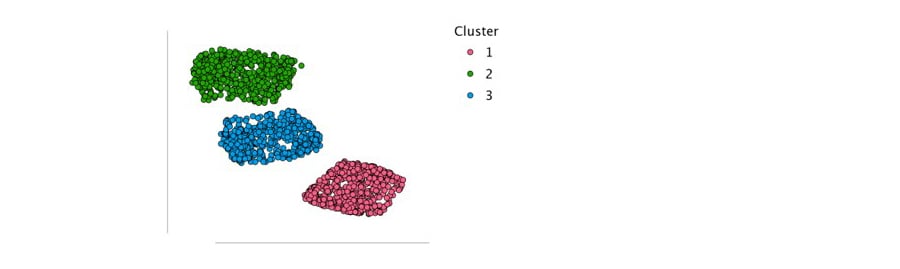
 Als je tevreden bent met de resultaten van het algoritme, is de volgende stap het toevoegen van de clusterbepalingen aan de gegevens. Dat doe je door in de interface de optie 'Voorspellingen toevoegen aan gegevens' aan te klikken en Cluster als kolomnaam in te vullen. Dat zorgt ervoor dat de resultaten van het clusteralgoritme worden toegevoegd aan de gegevens in een nieuwe kolom.

Interpretatie

Met de resultaten van het clusteralgoritme kun je een vervolganalyse uitvoeren om de clusters bedrijfsmatig te interpreteren. Dit kan bijvoorbeeld door beschrijvende statistieken van de kenmerken voor elke cluster uit te rekenen. Hiervoor ga je naar 'Beschrijvende statistiek' en sleep je alle kenmerken, behalve Locatie, naar het veld voor 'Variabelen'. Vervolgens sleep je de variabele Cluster naar het veld voor 'Splits'. Als laatste kun je in de uitvouwbare sectie 'Aanpasbare grafieken' de optie 'Boxplots' aanvinken.

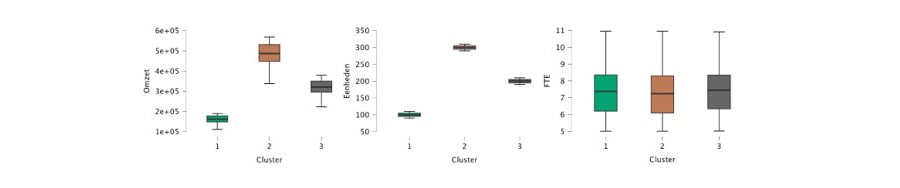
In de eerste twee figuren kun je zien dat de bedrijfslocaties in de eerste cluster zich onderscheiden door een relatief lage omzet en een laag aantal opslageenheden, terwijl de bedrijfslocaties in de tweede cluster een relatief hoge omzet en veel opslageenheden hebben. De derde cluster bevindt zich ergens tussen deze twee in. Dit suggereert dat de groepering van bedrijfslocaties wordt verklaard door de omvang van de locaties***. Het is interessant om op te merken dat, hoewel de bedrijfslocaties in drie clusters verschillen in omvang, deze gemiddeld evenveel fte’s aan de administratie hebben werken.

Deze resultaten kun je gebruiken om het risico op een fout in de gerapporteerde omzet per cluster in te schatten. Je zou bijvoorbeeld kunnen stellen dat de eerste cluster een relatief laag risico op fouten in de administratie heeft, omdat de bedrijfslocaties in deze cluster met een gemiddeld aantal fte's verantwoordelijk zijn voor de administratie van een lagere omzet. Omgekeerd zou je kunnen stellen dat de tweede cluster een relatief hoog risico op fouten in de administratie heeft, omdat deze met hetzelfde aantal fte's een hogere omzet moet verantwoorden. De derde cluster bevindt zich ergens tussen deze twee in en het risico op fouten in de administratie zou je daarom voor deze cluster als gemiddeld kunnen inschatten.

Acties

Op basis van de resultaten van deze analyse kun je de gestratificeerde steekproef uitvoeren. De clusters beschouw je daarbij als strata met een verschillend risicoprofiel. Hierdoor kun je overwegen om een relatief grote steekproef te nemen bij bedrijfslocaties die zijn toegewezen aan het stratum met een hoog risico op een fout in de gerapporteerde omzet. Tegelijkertijd kun je een relatief kleine steekproef nemen bij bedrijfslocaties die zijn toegewezen aan het stratum met een laag risico op een fout in de gerapporteerde omzet. Deze aanpak zorgt voor een efficiënte steekproefstrategie, omdat je daardoor waarschijnlijk minder werk hoeft te verrichten dan wanneer je geen stratificatie zou hebben toegepast.

Natuurlijk kun je deze workflow in JASP ook gebruiken om een clusteralgoritme toe te passen voor andere auditdoeleinden. Als je deze technieken zelf wilt gebruiken, dan kun je JASP gratis downloaden en installeren via www.jasp-stats.org.

 Noten
* De originele dataset is hier beschikbaar.
** Deze data zijn hier te vinden.
*** Door in de interface van het clusteralgoritme op de optie ‘Belang van kenmerken’ te klikken, kun je het algoritme laten bepalen welke kenmerken het meest dominant zijn bij het vormen van de clusters. In dit geval zijn dat de omzet, het advertentiebudget en het aantal opslageenheden, die allemaal positief samenhangen met de omvang van de bedrijfslocatie.

Referenties

• JASP Team. (2024). JASP (Versie 0.19.1)[Computer software].

• James, G., Witten, D., Hastie, T., Tibshirani, R., & Taylor, J. (2023). An Introduction to Statistical Learning with Applications in Python. Springer.

• Touw, P., & Hoogduin, L. (2012). Statistiek voor Audit en Controlling. Boom uitgevers Amsterdam.