De pilotsteekproef: een gids die je ook de verkeerde weg kan wijzen!
Deze column gaat over pilotsteekproeven. Hiervoor wordt vaak uit de (statistisch) losse pols een omvang van 25 voorgesteld. Deze column illustreert dat een kleine pilotsteekproef in een administratieve context kan leiden tot non-informatie.
Bij sommige schattingsmethoden voor het evalueren van steekproeven heeft het zin om vooraf een indicatie te hebben van de spreiding tussen de (nog te vinden!) foutbedragen. Als we die spreiding zouden weten, konden we uitrekenen hoeveel waarnemingen nodig waren om de maximale fout aan de (uitvoerings)materialiteit te laten voldoen. Om een indicatie van deze spreiding te krijgen wordt dan wel een pilotsteekproef aangeraden. Op basis van de geschatte spreiding in die pilotsteekproef wordt dan bepaald of, en zo ja hoeveel, aanvullende waarnemingen nodig zijn. Maar hoe groot kies je zo'n pilot? Vaak wordt dan het vertrouwde aantal van 25 van stal gehaald.
Wat kan hier mis gaan?
Een voorbeeld:
De te controleren populatie in geld bevat 4 procent posten met fouten. Dat betekent nog niet dat de geldpopulatie ook 4 procent fouten bevat want niet alle posten hoeven 100 procent fout te zijn. Een pilot van 25 posten zal naar verwachting één fout opleveren. Als dat gebeurt kunnen we een schatting maken van de spreiding tussen de foutbedragen en die gebruiken om de aanvullende steekproefomvang te bepalen.
Echter, de kans op nul fouten in een steekproef van 25 uit een populatie met 4 procent fouten is 0,36. Met 36 procent kans zal deze pilot dus nul posten met fouten opleveren. Maar de conclusie is dan dat er geen aanvullende waarnemingen meer nodig zouden zijn omdat de spreiding tussen de foutbedragen 0 is.
De kans dus dat deze pilot van 25 leidt tot een te kleine steekproef is 36 procent. Hierbij een tabel met meer uitkomsten (die laten zien dat het nóg erger kan):
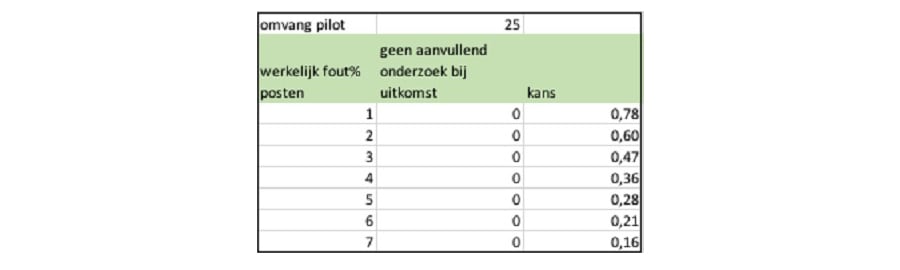
Hoe het dan wel moet: 'Sla de pilotsteekproef over!'
Al in de jaren tachtig van de vorige eeuw heeft prof. J. Kriens met collega's van de Universiteit van Tilburg* simulatiestudies gedaan op integraal gecontroleerde voorraden. Voorraad is een typisch voorbeeld van een populatie met fouten naar twee kanten waar je de spreiding tussen de foutbedragen nodig hebt voor de evaluatie. Om de noodzakelijke omvang vooraf in te kunnen schatten zou je die spreiding dus ook willen weten bij opzet van de steekproef. Stelden de auteurs voor een pilotsteekproef te doen? Nee, zij kwamen tot drie, andere, conclusies:
- dat bij zo'n 150 tot 180 waarnemingen men meestal voldoende fouten vindt voor een bruikbare schatting van de spreiding tussen de foutbedragen. Voor alle zekerheid adviseer ik daarom meestal 200 waarnemingen;
- dat er dan zelden aanvullende waarnemingen nodig zijn omdat achteraf blijkt dat de werkelijke spreiding voldoende nauwkeurig en betrouwbaar is geschat. Het is dus beter om de pilot over te slaan;
- dat hoe minder fouten de populatie bevat, des te meer waarnemingen er nodig zijn om zeker te weten dat een steekproef (met ook weinig fouten) representatief is. En andersom: een populatie met heel veel fouten kan met een kleinere steekproef (zeg, honderd waarnemingen) worden gecontroleerd.
Die derde conclusie heeft een interessante consequentie. Vaak zullen accountants op basis van het risicoanalysemodel de steekproef verkleinen als weinig fouten verwacht worden. Hier geldt juist dat bij weinig verwachte fouten de steekproef groter moet zijn. Het verschil is dat het risicoanalysemodel gebaseerd is op een toetsing (de stelling dat de populatie een materiële fout bevat wordt pas verworpen bij voldoende correcte waarnemingen) en we nu bezig zijn met een schatting (de accountant neemt aan dat de populatie geen materiele fout bevat, tenzij de steekproef te veel en te grote fouten oplevert). Doel van de steekproef is nu geen toets of de fout aanvaardbaar klein is, maar een zo nauwkeurig mogelijke schatting van de fout.
* Kriens, J. & Timmermans, H. & Wildenberg, H. & Kleijnen, Jack. (1989). Regression Sampling in Statistical Auditing: A Practical Survey and Evaluation. Tilburg University, Open Access publications from Tilburg University. 43. 10.1111/j.1467-9574.1989.tb01262.x.
Gerelateerd

Machine learning in de audit: stratificeren van bedrijfslocaties
In dit derde en laatste deel van een reeks columns over machine learning in de audit gaat het over clusteren. De auteurs laten zien hoe je met een open-source statistiekprogramma...

Machine learning in de audit: uitschieters bij vastgoedwaardering
Regressie is een vorm van machine learning met als doel het voorspellen van cijfers op basis van een aantal kenmerken. Met open-sourcesoftware kun je zonder programmeerkennis...

Machine learning in de audit: voorspellen van klantverloop
Het doel van machine learning is om voorspellingen te maken aan de hand van data. Binnen dit veld worden doorgaans drie hoofdtoepassingen onderscheiden: classificatie,...

De steekproefomvang ontmaskerd - deel 5
In vorige columns hebben we verschillende manieren besproken om tot een steekproefomvang te kunnen komen. Deze column is de laatste van de serie waarin we verschillende...

De steekproefomvang ontmaskerd - deel 4
Een accountant die gebruikmaakt van software om een steekproefomvang te berekenen, moet zeker weten dat die software dat goed doet. Daarvoor moet je de rekenmethode...
