Als een accountant wil vaststellen dat hij, met een aan zekerheid grenzende waarschijnlijkheid, kan afkeuren, heeft hij daarvoor dan een methodologie voorhanden?
Gangbaar bij een financiële controle is de methodologie om het gegevensgerichte deel van de controle als een goedkeuringsonderzoek in te richten. De uitkomst kan dan zijn "het is zonder meer mogelijk om goed te keuren" (groen) of "het is mogelijk om na correctie van de geprojecteerde fout goed te keuren” (oranje) of "er is uitgebreid aanvullend onderzoek nodig om eventueel te kunnen goedkeuren" (rood).
De kleuren die ik weergaf sluiten aan bij de “verkeerslichten” in de columns van Paul van Batenburg.
Minder gangbaar is het om het gegevensgerichte deel van een financiële controle niet als goedkeuringsonderzoek in te richten, maar als afkeuringsonderzoek. Misschien klinkt "afkeuringsonderzoek" wat vreemd, maar een afkeuringsonderzoek is in wezen het spiegelbeeld van een goedkeuringsonderzoek. Waar in het goedkeuringsonderzoek de maximale fout de materialiteit niet mag overschrijden om te kunnen goedkeuren, moet bij een afkeuringsonderzoek de minimale fout groter zijn dan de materialiteit om te kunnen concluderen tot afkeuring. Dat is onder meer terug te vinden bij de aanpak van de Europese Commissie: die keurt af als de minimale fout groter is dan 2 procent.

Deze manier van redeneren sluit aan bij wat in strafrechtelijke procedures gangbaar is: het afkeuringsmodel presenteert de omvang van de (mogelijke) fraude met een aan zekerheid grenzende waarschijnlijkheid.
Zoals gezegd gaat deze column over het gegevensgerichte deel van een controle en speelt zich dus af in een administratieve context. De IST-posities zijn dan de boekingen in de financiële administratie. De SOLL-posities moeten afgeleid worden uit een combinatie van primaire vastleggingen, uitkomsten van interviews, gegevens van derden et cetera.
Ik presenteer om te kunnen vergelijken beide methoden. Eerst de meest gebruikte methode, het goedkeuringsonderzoek, en daarna het afkeuringsonderzoek. Die laatste methode vind ik de meest geschikte methode als er sprake is van (het gegevensgerichte deel van) een fraudeonderzoek.

Goedkeuringsonderzoek

Deze column gaat over statistical auditing. Daarom ga ik ervan uit dat er een (gegevensgerichte) geldsteekproef is getrokken. Als de onderzoeker de kleinst mogelijke steekproef wil toepassen om te kunnen goedkeuren, gaat hij uit van een betrouwbaarheid van 95 procent en staat hij geen fouten toe in de steekproef, gegeven de onnauwkeurigheid (toegelaten afwijking) van het onderzoek. Elk element van de onderzochte populatie en dus ook elk element van de steekproef is a priori 'niet goed' en moet door onderzoek tot 'goed' worden opgewaardeerd.

De onderzoeker kan pas dan goedkeuren als hij zoveel goede elementen heeft gezien dat de maximale fout in de populatie kleiner is geworden dan de goedkeuringsgrens (de uitvoeringsmaterialiteit of de materialiteit). De onderzoeker heeft dan zoveel elementen tot 'goed' opgewaardeerd dat daardoor de maximale fout net de materialiteit onderschrijdt. Dus: de slechtste populatie is dan nog net goed genoeg.

Afkeuringsonderzoek

Ik ga (weer) uit van een (gegevensgerichte) geldsteekproef. De onderzoeker gebruikt (weer) een combinatie van betrouwbaarheid en toegelaten afwijking. Elk element van de onderzochte populatie en dus ook elk element van de steekproef is a priori 'niet fout' en moet door onderzoek tot 'fout' worden opgewaardeerd. Dit is het eerste deel van het spiegelbeeld.
Om het spiegelbeeld af te maken bij dit afkeuringsonderzoek: de onderzoeker kan pas dan afkeuren als de minimale fout in de populatie groter is dan de afkeuringsgrens (de uitvoeringsmaterialiteit of de materialiteit). De onderzoeker heeft dan zoveel, a priori 'niet foute' elementen tot 'fout' opgewaardeerd dat daardoor de minimale fout net de materialiteit overschrijdt. Dus: de 'beste' populatie is nog net te slecht.
Misschien overtollig: voldoende bewijs leveren dat er (nog niet) kan worden goedgekeurd is dus niet hetzelfde als afkeuren.
En net zo overtollig: voldoende bewijs leveren dat er (nog niet) kan worden afgekeurd is niet hetzelfde als goedkeuren.
Even een plaatje (met dank aan Paul van Batenburg), met toelichting, dat beide methoden illustreert.

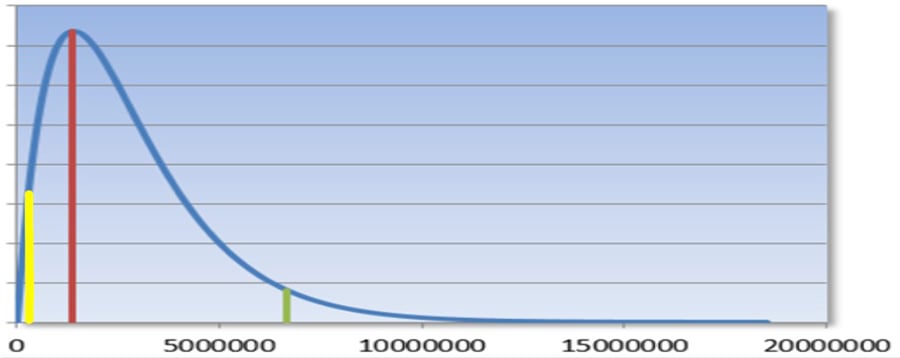
In dit plaatje zijn drie kritische plaatsen aangegeven. De rode lijn geeft de geprojecteerde of meest waarschijnlijke fout aan. De groene lijn geeft maximale fout aan (rechts ervan is de oppervlakte onder de kansverdeling van fouten in een populatie de kans op ten onrechte goedkeuren). De gele lijn geeft de minimale fout aan (links ervan is de oppervlakte onder de kansverdeling van fouten in een populatie de kans op ten onrechte afkeuren).

Afkeuringsonderzoek

Ik heb in deze column de wil om te kunnen afkeuren als drijfveer voor een fraudeonderzoek omschreven. Het model van een afkeuringsonderzoek zoals ik dat schetste is het spiegelbeeld van het model van een goedkeuringsonderzoek. Het voordeel van het afkeuringsmodel is dat de omvang van de (mogelijke) fraude met een aan zekerheid grenzende waarschijnlijkheid kan worden gepresenteerd. Dit is een mate van zekerheid die past bij strafrechtelijke onderzoeken.
Anders (gedeeltelijk in het Engels) gezegd:

• Een goedkeuringsonderzoek heeft als uitgangspunt: Guilty until proven innocent.
• Een afkeuringsonderzoek heeft als uitgangspunt: Innocent until proven guilty.